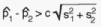|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 Sampling and Non-sampling ErrorsThe statistical quality or reliability of a survey may obviously be influenced by the errors that for various reasons affect the observations. Error components are commonly divided into two major categories: Sampling and non-sampling errors. In sampling literature the terms "variable errors" and "bias" are also frequently used, though having a precise meaning which is slightly different from the former concepts. The total error of a survey statistic is labeled the mean square error, being the sum of variable errors and all biases. In this section we will give a fairly general and brief description of the most common error components related to household sample surveys, and discuss their presence in and impacts on this particular survey. Secondly, we will go into more detail as to those components which can be assessed numerically.
Error Components and their Presence in the Survey The variance or the standard error does not tell us exactly how great the error is in each particular case. It should rather be interpreted as a measure of uncertainty, i.e. how much the estimate is likely to vary if repeatedly selected samples (with the same design and of the same size) had been surveyed. The variance is discussed in more detail in section 6.2.
(2) Non-sampling errors is a "basket" comprising all errors which
are not sampling errors. These type of errors may induce systematic bias
in the estimates, as opposed to random errors caused by sampling errors.
The category may be further divided into subgroups according to the various
origins of the error components:
Sampling Error - Variance of an Estimate Generally, the prime objective of sample designing is to keep sampling error at the lowest level possible (within a given budget). There is thus a unique theoretical correspondence between the sampling strategy and the sampling error, which can be expressed mathematically by the variance of the estimator applied. Unfortunately, design complexity very soon implies variance expressions to be mathematically uncomfortable and sometimes practically "impossible" to handle. Therefore, approximations are frequently applied in order to achieve interpretable expressions of the theoretical variance itself, and even more to estimate it.
In real life practical shortcomings frequently challenge mathematical comfort.
Absence of sampling frames or other prior information forces one to use
mathematically complex strategies in order to find feasible solutions. The
design of the present survey - stratified, 4-5 stage sampling with varying
inclusion probabilities - is probably among the extremes in this respect,
implying that the variance of the estimator (5.2) will be of the utmost
complexity - as will be seen subsequently. The PSU (s,k) variance components in the latter formula have a structure similar to the stratum one, as is realized by regarding the PSUs as separate "strata" and the cells as "PSUs". Again, another variance component emerges for each of the cells, the structure of which is similar to the preceding one. In order to arrive at the "ultimate" variance expression yet another two or three similar stages have to be passed. It should be realized that the final variance formula is extremely complicated, even if simplifying modifications and approximations may reduce the complexities stemming from the 2nd - 5th sampling stages. It should also be understood that attempts to estimate this variance properly and exhaustively (unbiased or close to unbiased) would be beyond any realistic effort. Furthermore, for such estimation to be accomplished certain preconditions have to be met. Some of these conditions cannot, however, be satisfied (for instance: at least two PSUs have to be selected from each stratum comprising more than one PSU). We thus have to apply a more simple method for appraising the uncertainty of our estimates. Any sampling strategy (sample selection approach and estimator) may be characterized by its performance relative to a simple random sampling (SRS) design, applying the sample average as the estimator for proportions. The design factor of a strategy is thus defined as the fraction between the variances of the two estimators. If the design factor is, for instance, less than 1, the strategy under consideration would be better than SRS. Usually, multi-stage strategies are inferior to SRS, implying the design factor being greater than 1.
The design factor is usually determined empirically. Although there is no
overwhelming evidence in its favour, a factor of 1.5 is frequently used
for stratified, multi-stage designs. (The design factor may vary among survey
variables). The rough approximate variance estimator is thus:
Table A.12 Standard error estimates for proportions (s and p are specified as percentages).
Confidence Intervals A confidence interval is a formal measure for assessing the variability of survey estimates from such hypothetically repeated sample selections. The confidence interval is usually derived from the survey estimate itself and its standard error: Confidence interval: [p - c s, p + c s] where the c is a constant which must be determined by the choice of a confidence coefficient, fixing the probability of the interval including the true, but unknown, population proportion for which p is an estimate. For instance, c=1 corresponds to a confidence probability of 67%, i.e. one will expect that 67 out of 100 intervals will include the true proportion if repeated surveys are carried out. In most situations, however, a chance of one out of three to arrive at a wrong conclusion is not considered satisfactory. Usually, confidence coefficients of 90% or 95% are preferred, 95% corresponding to approximately c=2. Although our assessment as to the location of the true population proportion thus becomes less uncertain, the assessment itself, however, becomes less precise as the length of the interval increases.
Comparisons between groups
We will assume that the estimate
Hypothesis: p1 = p2
In case the test rejects the hypothesis we will accept the alternative as
a "significant" statement, and thus conclude that the observed
difference between the two estimates is too great to be caused by randomness
alone. However, as is the true nature of statistical inference, one can
(almost) never draw absolutely certain conclusions. The uncertainty of the
test is indicated by the choice of a "significance level", which
is the probability of making a wrong decision by rejecting a true hypothesis.
This probability should obviously be as small as possible. Usually it is
set at 2.5% or 5% - depending on the risk or loss involved in drawing wrong
conclusions.
The test implies that the hypothesis is rejected if
Significance level c-value
------------------ -------
2.5% 2.0
5.0% 1.6
10.0% 1.3
As is seen, the test criteria comprise the two standard error estimates
and thus imply some calculation. It is also seen that smaller significance
levels imply the requirement of larger observed differences between sub-groups
in order to arrive at significant conclusions. One should be aware that
the non-rejection of a hypothesis leaves one with no conclusions at all,
rather than the acceptance of the hypothesis itself.
Non-response Furthermore, up to 4 call-backs were applied if selected respondents were not at home. Usually the data collectors were able to get an appointment for a subsequent visit at the first attempt, so that only one revisit was required in most cases. Unit non-response thus comprises refusals and those not being at home at all after four attempts. Table A.13 shows the net number of respondents and non-responses in each of the three parts of the survey. The initial sizes of the various samples are deduced from the table by adding responses and non-responses. For the household and RSI samples, the total size was 2,518 units, while the female sample size was 1,247. It is seen from the bottom line that the non-response rates are outstandingly small compared to the "normal" magnitudes of 10 - 20% in similar surveys. Consequently, there should be fairly good evidence for maintaining that the effects of non-response in this survey are insignificant. Table A.13 Number of (net) respondents and non-respondents in the tree parts of the survey
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 al@mashriq 960428/960710 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
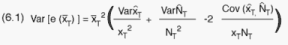
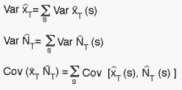
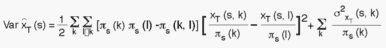
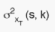 the variance of the PSU (s,k) unbiased estimate
the variance of the PSU (s,k) unbiased estimate 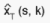 . The variance of
. The variance of  is obtained
similarly by substituting x with N in the above formula. The stratum covariance
formula is somewhat more complicated and is not expressed here.
is obtained
similarly by substituting x with N in the above formula. The stratum covariance
formula is somewhat more complicated and is not expressed here.
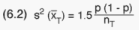
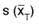 or briefly s, is called the standard
error, and is tabulated in table A.12 for various values of p and n.
or briefly s, is called the standard
error, and is tabulated in table A.12 for various values of p and n.
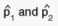 , respectively, while the unknown true proportions
are denoted p1 and p2. The corresponding standard error estimates are s1
and s2. The problem of inference is thus to evaluate the significance of
the difference between the two sub-group estimates: Can the observed difference
be caused by sampling error alone, or is it so great that there must be
more substantive reasons for it?
, respectively, while the unknown true proportions
are denoted p1 and p2. The corresponding standard error estimates are s1
and s2. The problem of inference is thus to evaluate the significance of
the difference between the two sub-group estimates: Can the observed difference
be caused by sampling error alone, or is it so great that there must be
more substantive reasons for it?
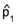 is the larger of the two proportions observed.
Our problem of judgement will thus be equivalent to testing the following
hypothesis:
is the larger of the two proportions observed.
Our problem of judgement will thus be equivalent to testing the following
hypothesis: