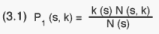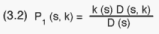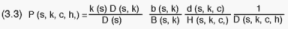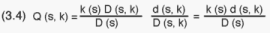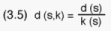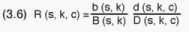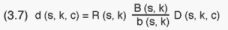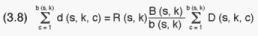3 West Bank Sample Design
The design for the West Bank is a multistage stratified one. As compared
to Gaza, more prior information was available on the West Bank localities,
providing opportunities for improving the sample design - at least concerning
the practical preparatory work involved. The main features of the design
are outlined in the following sections.
Stratification of Primary Sampling Units (PSUs)
The localities as defined by Benvenisti (adjusted for Camp Areas included
in other types of localities) are the PSUs. The PSUs were stratified according
to location (7 sub-districts) and status (5 categories, i.e. District Capitals
(DC), Other Towns (OT), Developed Villages (DV), Underdeveloped Villages
(UV) and Refugee Camps (RC)). The number of strata are thus 32 (3 of the
theoretical 35 combinations of sub-district and status are empty). Table
A.6 shows estimates of the strata populations:
Table A.6 Population estimates for West Bank strata. (Individuals all ages. Benvenisti/ estimates for 1987. "Permanent" population)
| Status |
| Sub-district | DC | OT | DV | UV | RC |
| Bethlehem | 32,800 | 18,300 | 23,100 | 30,000 | 10,200 |
| Hebron | 79,100 | 44,000 | 68,600 | 24,100 | 8,300 |
| Jenin | 16,800 | 36,000 | 36,900 | 56,700 | 14,600 |
| Jericho | 12,500 | . | . | 4,100 | 3,400 |
| Nablus | 80,800 | . | 42,600 | 41,800 | 26,200 |
| Ramallah | 24,800 | 35,100 | 25,200 | 87,100 | 15,500 |
| Tulkarem | 19,600 | 29,600 | 67,500 | 35,800 | 15,300 |
Although these estimates may be somewhat inaccurate, they cannot be dispensed
with for want of more reliable alternatives. We assume they give a reasonably
fair representation of the relative proportions of localities and strata,
which for sampling purposes is the most relevant information.
Allocation of Household Sample on Strata
The sample size for the West Bank is 1,040 households (from which both the
sample of 1,040 individuals and 520 women also are derived). The allocation
of the household sample among strata is proportionate to the estimated population
size. The allocation is shown in Table A.7.
Table A.7 Allocation of West Bank household sample on strata (proportionate allocation)
| Status | |
| Sub-district | DC | OT | DV | UV | RC | Total |
| Bethlehem | 32 | 18 | 23 | 31 | 9 | 113 |
| Hebron | 77 | 42 | 67 | 24 | 8 | 218 |
| Jenin | 17 | 35 | 35 | 56 | 14 | 157 |
| Jericho | 13 | . | . | 5 | 4 | 22 |
| Nablus | 78 | . | 40 | 42 | 26 | 186 |
| Ramallah | 23 | 34 | 25 | 85 | 15 | 182 |
| Tulkarem | 18 | 29 | 65 | 36 | 14 | 162 |
| Total | 258 | 158 | 255 | 279 | 90 | 1,040 |
Selection of Sample PSUs (1st stage)
Sample PSUs were selected from each stratum with a probability proportionate
to population size. In order to determine the 1st stage inclusion probability,
we need the following variables (all referring to individuals, Benvenisti
estimates):
N(s,k) = Population total for PSU (s,k)
N(s) = Population total s-th stratum (table A.6)
N = Population total (West Bank)
The first stage inclusion probability for PSU (s,k) is approximately:
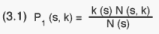
in which k(s)k(s) is the number of PSUs selected from the s-th stratum. In case
k(s)=1, the equality above is exact. The approximation occurs for k(s)>1,
as 2nd order (and higher) probabilities are assumed negligible. The number
of PSUs to be selected, the k(s)'s, has been decided like this in order
to avoid situations where the number of sample households of a PSU exceeds
the total number of PSU households. Thus, for each stratum both the household
sample size, the total number of PSUs and the size of the various PSUs have
been considered.
In our design the household, not the single individual, is the ultimate
unit of selection. If the average size of households is equal for all PSUs,
which is a fairly realistic assumption, (3.1) can be expressed thus:
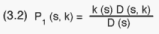
in which D(s,k) is the total number of households in PSU (s,k), and D(s)
the corresponding total for the s-th stratum.
The number of sample PSUs selected from each of the strata are shown in
table A.8. The total number of sample PSUs is 45.
Table A.8 Total (K(s)) and sample (k(s)) number of PSUs in the West Bank strata
| Status |
| DC | OT | DV | UV | RC |
| Sub-district | K(s) | k(s) | K(s) | k(s) | K(s) | k(s) | K(s) | k(s) | K(s) | k(s) |
| Bethlehem | 1 | 1 | 2 | 1 | 5 | 1 | 24 | 2 | 3 | 1 |
| Hebron | 1 | 1 | 3 | 1 | 14 | 3 | 47 | 2 | 2 | 1 |
| Jenin | 1 | 1 | 4 | 1 | 9 | 1 | 44 | 3 | 2 | 1 |
| Jericho | 1 | 1 | . | . | . | . | 9 | 1 | 2 | 1 |
| Nablus | 1 | 1 | . | . | 15 | 1 | 34 | 2 | 3 | 1 |
| Ramallah | 1 | 1 | 6 | 1 | 14 | 1 | 69 | 4 | 4 | 1 |
| Tulkarem | 1 | 1 | 3 | 1 | 28 | 3 | 45 | 2 | 2 | 1 |
Selection of Cells, Housing Units and Households
As in Gaza, there were no sampling frames available for the selection of
households in the West Bank PSUs. Thus it was convenient to introduce two
further sampling stages. At the 2nd stage sample PSUs were subdivided into
cells, and samples of cells were selected by simple random sampling from
the respective PSUs. Housing units were selected at the 3rd stage, and,
finally, the samples of households (4th stage) were selected from the sample
of housing units. The procedures operate exactly as for Gaza and are thus
not repeated. However, the mathematics for sample allocation are not the
same. This will be dealt with in the next section.
Inclusion Probabilities
Adopting the same notations as for the Gaza design, the overall inclusion
probability for an arbitrary West Bank household (s,k,c,h,d) is:
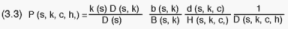
In (3.3) it remains to determine the b(s,k)'s and the d(s,k,c)'s. For the
same reasons as for Gaza, it is practically impossible to have an overall
epsem design. For the purpose of allocating each stratum sample of households
(or housing units) among PSUs, let us temporarily disregard the cell and
housing unit stages of selection, assuming that households can be selected
directly within PSUs. In this case the household inclusion probability can
be written thus:
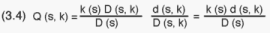
where d(s,k) is the household sample size of PSU (s,k). In order to have
an epsem design, it is required that Q(s,k) be a constant, independent of
which PSUs (k) are selected at the 1st stage. For this to be true it can
be seen from (3.4) that the d(s,k)s have to be equal for all selected PSUs
within the stratum, i.e. the stratum sample of households, denoted d(s),
has to be equally divided among the sample PSUs:
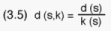
Having thus determined the household sample allocation among PSUs within
the strata, the next step is to allocate the various PSU subsamples among
PSU cells. The housing unit selection stage is still disregarded. The (conditional)
inclusion probability for an arbitrary household (s,k,c,d) within PSU (s,k)
is:
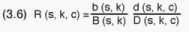
In order to have a local (within PSU) epsem design, the R(s,k,c) must be
a constant, i.e. independent of c. However, having two unspecified variables
- b(s,k) and d(s,k,c) - and only one equation for determining them, we are
free to specify any of them independently. To make a proper choice one should,
however, appraise both cost and sampling error components. While budgetary
constraints might suggest that the number of cells to be selected should
be "small", considerations of sampling error induce no obvious
choice. The sampling error can be split into two components reflecting within
cell variations and variations between cells, respectively (variations refer
to the survey variables). In general, preference should be given to the
dominating component of variation. Thus, great between cell variations imply
a large number of cells (and few households per cell) to be included, while
great within cell variations suggest a smaller number of cells (and more
households per cell).
As no prior information about the magnitude of the components of variation
was available, further elaboration of sampling error considerations would
obviously have been both speculative and questionable. We thus leave this
discussion in order to address a more practical approach.
It was decided above that 45 PSUs be included in the 1st stage sample, implying
on average approximately 23 households to be selected within each of the
PSUs. To avoid concentration of all PSU interviews to one single area it
was also decided to include at least 2 sample cells in every PSU. An average
sample size per cell of 5-10 households was convenient for practical reasons
as well. Thus the number of cells selected in each of the sample PSUs was
for the majority of PSUs 2-5. There are, however, a few exceptions where
only 1 or more than 5 cells were selected, depending on both the total number
of cells and the household sample size for the PSU. In practice the b(s,k)s
are roughly proportionate to the PSU total number of cells, B(s,k). The
allocation of sample cells among PSUs is shown in table A.9.
Having thus decided the number of sample cells in each of the PSUs it remains
to determine the allocation of the PSU household sample among cells. According
to (3.6) this allocation obviously has to be proportionate in order to have
a local (within PSU) epsem design. As stated previously, the latter requires
R(s,k,c) to be a constant independent of the cell (c) under consideration.
Thus, in R(s,k,c) we may omit the index c and reformulate (3.6):
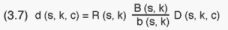
In order to calculate R(s,k) for each of the sample PSUs we take the sum
for every (s,k) of both sides of (3.7):
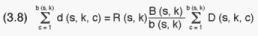
The left hand side adds to the PSU sample size, d(s)/k(s). On the right
hand side all statistics are known except for the constant R(s,k). Hence
R(s,k) is determined, and the individual d(s,k,c)s can be calculated from
(3.7), concluding the sample allocation calculations. The d(s,k,c)s arrived
at also determine the number of housing units selected from each cell.
The final household and cell sample allocation is displayed in table A.9
for the selected PSUs.
Before concluding this section, we return to the overall inclusion probability
(3.3), to see how this can be calculated.
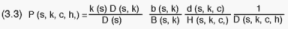
The first fraction on the right hand side is the 1st stage inclusion probability.
At the planning stage the numbers of PSU and stratum households, the D(s,k)s
and D(s)s, were not available. Instead, the Benvenisti estimates6 of the
total population figures were used (equation (3.1)). The second fraction
is the 2nd stage inclusion probability which can be calculated from the
figures in table A.9. To calculate the third fraction, the d(s,k,c)s are
taken from the finally observed (net) sample, and the H(s,k,c)s are estimated
by formula (2.4) in the Gaza design section. The last fraction - the 4th
stage inclusion probability - is determined by the sample observations of
the D(s,k,c,h)s.
Table A.9 Total and sample number of cells, and household sample size in the West Bank sample PSUs
| | Number of cells |
Stratum
District/
Status | PSU name (Locality)
(s,k) | Total
B(s,k) | Sample
b(s,k) | Household sample size
d(s,k) |
| Bethlehem |
| DC | Bethlehem | 42 | 6 | 32 |
| OT | Beit Sahour | 22 | 3 | 18 |
| DV | Beit Fajjar | 8 | 3 | 23 |
| UV | Artas | 4 | 4 | 16 |
| Husan | 4 | 2 | 15 |
| RC | El Daheisha | 13 | 2 | 9 |
| Hebron |
| DC | Hebron | 107 | 10 | 77 |
| OT | Yatta | 21 | 5 | 42 |
| DV | Beit Ummar | 7 | 4 | 23 |
| El Dhahiriya | 8 | 6 | 22 |
| Kharass+Nuba | 7+3 | 3+1 | 14+8 |
| UV | El Rihiya | 2 | 2 | 12 |
| Sair | 8 | 2 | 12 |
| RC | El Fawar | 7 | 2 | 8 |
| Jenin |
| DC | Jenin | 21 | 3 | 17 |
| OT | Ya'abad | 12 | 5 | 35 |
| DV | Jalame | 3 | 3 | 35 |
| UV | A'qabe | 5 | 3 | 18 |
| Jaba'a | 6 | 3 | 19 |
| Kfar Dan | 4 | 3 | 19 |
| RC | Mukayam Fara'a | 8 | 3 | 14 |
| Jericho |
| DC | Jericho | 21 | 3 | 13 |
| UV | Nue'ima | 5 | 1 | 5 |
| RC | Jericho RC | 6 | 1 | 4 |
| Nablus |
| DC | Nablus | 106 | 10 | 78 |
| DV | A'sira Shimaliya | 8 | 5 | 40 |
| UV | Beit Dajan | 5 | 4 | 22 |
| Salem | 3 | 3 | 20 |
| RC | Balata RC | 19 | 4 | 26 |
| Ramallah |
| DC | Ramallah | | | |
| OT | Silwad | 8 | 5 | 34 |
| DV | Singel | 5 | 5 | 25 |
| UV | A'nata | 6 | 4 | 22 |
| Deir Jerir | 4 | 4 | 21 |
| Kafr Malek | 4 | 4 | 22 |
| Qibya | 3 | 3 | 20 |
| RC | Am'ari | 10 | 3 | 15 |
| Tulkarem |
| DC | Tulkarem | 43 | 3 | 18 |
| OT | Qalqilya | 37 | 5 | 29 |
| DV | Allar | 6 | 4 | 21 |
| Habla | 5 | 5 | 22 |
| Kafr Qadum | 4 | 4 | 22 |
| UV | Dannabe | 5 | 3 | 18 |
| Shufa | 2 | 2 | 18 |
| RC | Nur el Shams | 5 | 2 | 14 |
|